Introduction
Listening to stories is the first literary experience for children, where they can be transported to another place, transform themselves into different characters or create new horizons for imagination and creativity. We all remember some children’s story that evokes a pleasant memory, but we rarely had the experience of living one of these stories linked to curricular content related to scientific disciplines, such as mathematics.
Storytelling is a fundamental didactic mediator in children’s learning that facilitates the conveyance of symbolic messages in a playful and entertaining way, while stimulating their curiosity and imagination, elements that can be considered essential for the learning of content related to scientific disciplines through enquiry (Bevins & Price, 2016).
There is a wealth of research using stories as a learning tool and it facilitates us to go through different learning objectives, especially at an early age. Storytelling provides different elements to work on in the infant classroom, ranging from language development to working with pictures, as well as a wide range of possibilities that are foreseen within the fields that make up the official curriculum (Decreto 17, 2008).
Some of these specific approaches in the early stages of school can be the production of stories with a structured narrative, following an intervention based on reading and reconstructing stories (Borzone, 2005), or on the knowledge of scientific phenomena from representations (Kalogiannakis et al., 2017) or aspects focused on social emotions and feelings, creating a scenario where it is easy to name and recognise them (Sánchez et al., 2018). Storytelling can be a tool to “help generate and develop the necessary behaviours to increase participation and emotional expression, both in normal life situations and in situations of conflict or crisis” (Correa, 2002, p. 140).
From the point of view of early mathematics education, research in mathematics didactics has gained relevance in the last two decades, giving strength to a content formation adapted to the personal characteristics of children at this educational stage, paying special attention to the resources used in the classroom, and providing evidence showing that early mathematical skills form the basis for later learning (Claessens & Engel, 2013). The level of early mathematical competence development is positively related to verbal, spatial and memory skills (Locuniak & Jordan, 2008; Mazzoco & Thompson, 2005).
Mathematics instruction should be motivating in the early years, in order to engage children in problem solving (National Association for the Education of Young Children [NAEYC] & National Council of Teachers of Mathematics [NCTM], 2002). Teaching at these stages should facilitate the learning of mathematical content, while encouraging a positive approach to learning (Ginsburg & Golbeck, 2004), based on the creation of an appropriate mathematical environment that leads to experiences through manipulation (Dienes, 1990). The design of classroom situations arousing curiosity leads to the development of the ability to be creative (Casey, 2011); the teacher through the way he/she implements activities presents situations that promote children’s analytical and reasoning skills, facilitating their active participation (Jacobi-Vessels et al., 2016).
We should forget the need for adequate competence in linguistic communication in the learning of mathematics, a situation where working with stories can contribute through comprehensive reading and the correct expression of the results obtained. At this age, it is important to use activities that link the different content areas with the natural language, so that children can expand their oral language through listening and interaction with others. Additionally,
storytelling fits in perfectly with their symbolic play, as stories are represented through a deferred imitation thereof, and it allows them to foster their capacity for abstraction by understanding values such as “evil, goodness, greed, generosity, etc.”, to experience their feelings about the story by expressing their sympathies and antipathies towards the characters (Marín, 1999, p. 29).
Reading stories can facilitate children’s word knowledge in a context of number sense instruction (Hassinger-Das et al., 2015). The use of stories as a tool for learning mathematics shows different achievements in educational research. Whitin and Whitin (2004) point to storybooks as a good resource for connecting mathematical content with real-life situations. Reading stories can facilitate moments where logic and problem solving are worked on (Saá, 2002). The scenario provided by a story allows us to work with objects with which children can interact, thus acquiring logical-mathematical skills (Alsina, 2012).
Children build mathematical knowledge with positive attitudes by using stories as a means to imagine scenarios, where characters solve problems (Keat & Wilburne, 2009). The creation of connections between different situations gives rise to meaning in mathematical ideas, giving children a start in constructing generalisations from observation (Haylock & Cockburn, 2013).
Barrera (2015) presents a possibility of working on different mathematical contents in a contextualised way in real situations (counting, operations, among others) by constructing a storybook, which can be used from the third year of primary education onwards. Colomer and Ramos (2002) designed a research using fairy tales to work on mathematical content at an early stage, while Aymerich (2010) presented a review of which stories can be useful for working on mathematical content. More specifically as for the learning of a specific content, Rodríguez and Fernández (2016) construct a story to work on the decimal decomposition of numbers. The use of reading in a specific context of a school subject poses as a difficulty its instrumentalisation (Cerrillo, 2007), a fact that must be prevented from the design of the educational intervention, aiming at the creation of realities and contexts that are not far from the essence of the chosen reading.
Finally, we would like to mention an issue raised in didactic research in relation to two covariates, gender and age, assuming that they may influence early mathematics learning. Gender invariance in mathematics learning is widely explored at higher levels, however, studies in Early Childhood Education (EI, as per its Spanish acronym) are not as frequent (Aragón et al., 2013; Arens et al., 2016; Navarro et al., 2010). Any possible differences or similarities in performance according to gender can be considered from three approaches, arithmetic and spatial skills (Bakker et al., 2019; Nowell & Hedges, 1998; Reilly et al., 2017), problem solving strategies (Laski et al., 2013) or the influence of the social and cultural environment (Makosz et al., 2019; Nguyen & Ryan, 2008). However, we believe they are not disjunct situations but that both may or may not lead to differences in mathematics learning because of the intrinsic relationship they have with their objectives and content.
With regard to age, it is common for children in the infant classroom to have a chronological age that is different from their maturational age; in this sense, it is thus reasonable to think that learning outcomes will be conditioned by this variable. Research shows that chronological age may be related to numeracy skills (Nanu et al., 2020), and even that “students younger than average for their grade are more likely to perform poorly in mathematics” (Rodriguez, 2016, p. 5).
Therefore, storytelling is seen as a didactic tool in early ages, which facilitates the design of a motivating didactic scenario allowing a holistic work for the achievement of the teaching-learning objectives.
Objective
In the early stages of schooling, finding elements that motivate children to learn is a constant challenge, while creating situations where mathematical content is given strength at the same time. For this reason, we wanted to combine two focuses attention, presented in the background: reading the story and logical-mathematical learning. The main objective is to show the usefulness of storytelling in the early learning of mathematics, from the development of activities based on their reading; to this end, we set ourselves specific objectives in this work: (1) to adapt The Ugly Duckling, setting up a scenario for the development of logical-mathematical thinking from the scenes of the story; (2) to determine whether there are aspects of mathematical competence achievement that differ between children who learned using the stories and those who did not, and (3) to analyse possible gender and age differences in early mathematical learning.
Method
Given the characteristics of the research, a quasi-experimental cross-sectional design with a quantitative approach and a control group was defined.
Participants
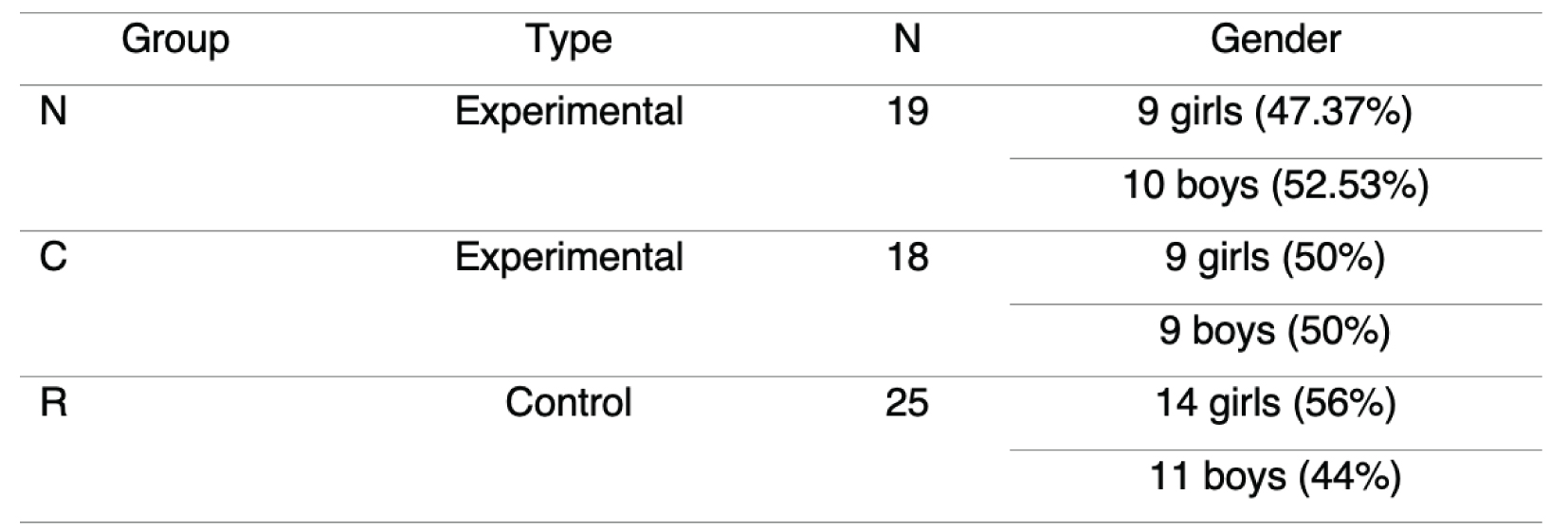
The sample of Childhood Education (EI) students (n=62) belonged to two state-subsidised schools located in the centre of Madrid. Median age in all groups at the start of the intervention is 5 years and 9 months.
The experimental and control groups were chosen randomly (table 1), but the groups were pre-formed.
Table 1
Distribution of students in the control and experimental groups
Instrument
In order to establish homogeneity in the level of mathematical knowledge within the groups, an initial assessment was designed with an ad hoc test administered individually, with 9 questions on the different logical-mathematical contents included in the stage curriculum: comparison (V1), classification (V2), correspondence (V3), serial sequences (V4), verbal counting (V5), structured counting (V6, V7), resultant counting (V8) and knowledge of number (V9).
Post-intervention outcomes were measured with the Spanish version of the Test de Evaluación Matemática Temprana (TEMT, as per its Spanish acronym) (Navarro et al., 2011). It is an individual test, designed to assess the level of mathematical competence in children aged between 4 and 7. The test has three versions (A, B and C), of 40 items each, grouped into 8 subtests (four of logical skills, P1 to P20; and four of numerical skills, P21 to P40) of 5 items each. For this intervention, the same version (A) was used for all children. The internal consistency of the TEMT is high (α = .95) both for the total scale and for the two subscales logical (α = .94) and numerical (α = .93). The application was done by a single researcher, trained in the use of this instrument, and the application time was between 20 and 30 minutes for each student.
The instrument facilitates the construction of a direct score, defined as a level of mathematical competence (NCM, as per its Spanish acronym), assigning each item a value of 1, and thus obtaining five levels A, B, C, D and E, which are labelled as "very good, good, moderate, low and very low" for each student, calculated in relation to the score obtained by his or her group.
The sample falls within age group III of the TEMT manual (Navarro et al., 2011).
Procedure
The procedure was designed jointly by the teaching staff of both schools. This makes it easier for researchers to focus on the specific domain and identify the real needs in the classroom (Cai et al., 2016).
For this design, the methodological principles of the EI stage have been taken into account, starting from the level of development of the student, the principle of activity and the key role played by the student, with meaningful learning in a globalised environment.
The first step was a diagnosis in the two classrooms that allowed us to find out the mathematical content skills each of the children had. The intention here was to detect possible difficulties and to ensure a homogeneous starting point in both groups.
The second step was the design of didactic situations (Brousseau, 1998) adapted to the reality of the students with whom we were going to work. The story selected was The Ugly Duckling (Andersen, 1843). We considered the use of a fairy tale to be an optimal choice because of its structural characteristics and because the children knew the story beforehand.
From the analysis of the original story of the tale, we analysed which scenes (table 2) could be used to work with mathematical content at this stage, in order to develop well-planned activities where this content is not isolated (Cascallana, 1988). One of the essentials elements in a story are the functions of the characters (Propp, 1981); in this case, they are going to determine the design of each activity based on the action they undertake. The story of The Ugly Duckling has a main character who acts according to a quest. The hero moves away from the familiar, to have different adventures that will focus us on the mathematical activity, to return later to his place with new learning. This three-phase structure of the story (Campbell, 1984) makes the story an ideal space for activities of an individual and collective nature, without the need for an adaptation of the story cycle.
Table 2
Scenes from the story and mathematical contents that were worked on

While the story is read, other content was also worked on verbally during the assembly. Some examples of text specifically used to design activities that required movement around the classroom (table 3). Integrating movement into mathematics learning has a positive effect on students’ enjoyment and engagement (Riley et al., 2017). This is content that the children already know beforehand and we seek to reinforce and consolidate it.
Table 3
Story text and mathematical content developed in groups

Thirdly, the structure of the implementation in the sessions was designed by alternating individual and group work. This work was carried out as materials were constructed simultaneously. The aim was to use materials not specific to didactics, but made for the occasion from objects from the child’s everyday life. The criterion that guided the choice was to have “a material with which to carry out activities in which the student is an active and participatory agent in the teaching-learning process” (Rodríguez & Fernández, 2016, p. 72).
As for staging, two considerations were taken into account: firstly, the proposals had to be adapted to the dynamics carried out by the teacher during the school day and secondly, this planning had to be flexible, in order to adapt to the needs of the children.
Oral narration of the story by the teacher is the first stage in the classroom. The children listen to the story as they are shown the illustrations, either on paper or digitally. The use of illustrations captures attention and it also enhances comprehension and memory in children (Follmer & Semb, 2008). When the children participate or ask questions, reading stops to ask them, and these questions “are extremely helpful when using the story as a learning tool, as they allow us to follow the thread of the children’s understanding and acquisition of the contents that appear in the story” (Marín, 2013, p. 9). How the teacher incorporates these questions into the storytelling will be his or her most important task, because it will make the learner nurture and increase his or her curiosity because “the story is not only to entertain, but to cause and be the cause of revolutions. One does not narrate only to know more, one narrates to learn to ask questions and to generate more and better questions” (Agudelo, 2016, p.14).
Once the teacher has finished the story, the storytelling starts again, but this time each scene is reinforced by the use of the different teaching materials. The aim is to make the mathematical content to be worked on perceptible; this phase is repeated every working day in each of the activities.
Results
The initial diagnosis results show that there are no differences between the control and experimental groups on any of the items, so it can be considered an equivalent control group design. Table 4 shows the p-values corresponding to the Chi-square test, where the null hypothesis states that there is no difference in the responses (percentage of correct answers) between the control and experimental groups.
Table 4
Initial diagnostic results

Note: a=constant variable; all are correct in both groups.
Furthermore, we can point out that the level of success performance in each of them is always above 50%, as can be seen in figure 1.
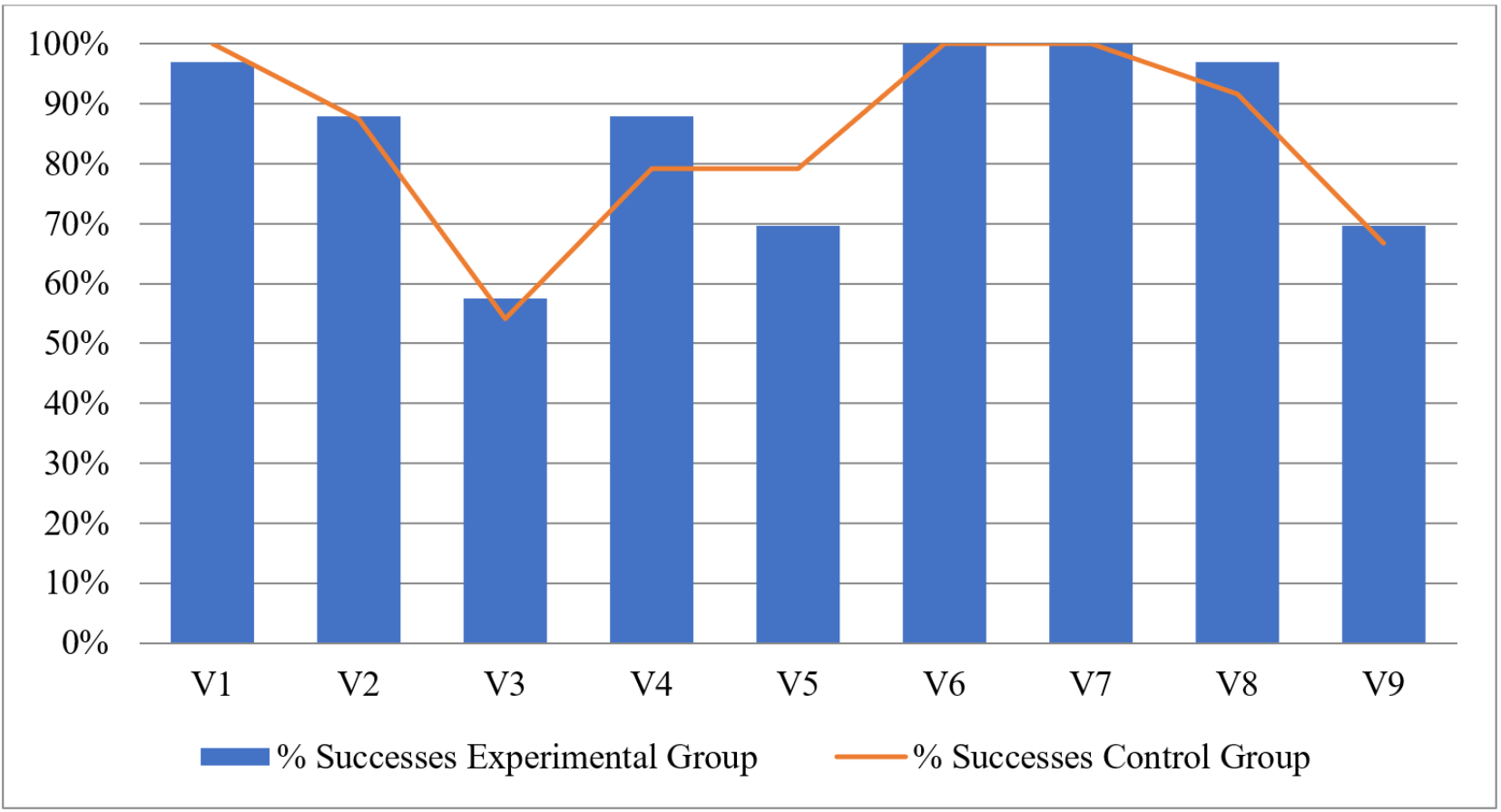 Figure 1
Initial diagnosis results
Figure 1
Initial diagnosis results
As for the results after the intervention, the percentages of success in the experimental and control groups in each of the skill blocks (figures 2 and 3) show better results in almost all the items for the experimental group.
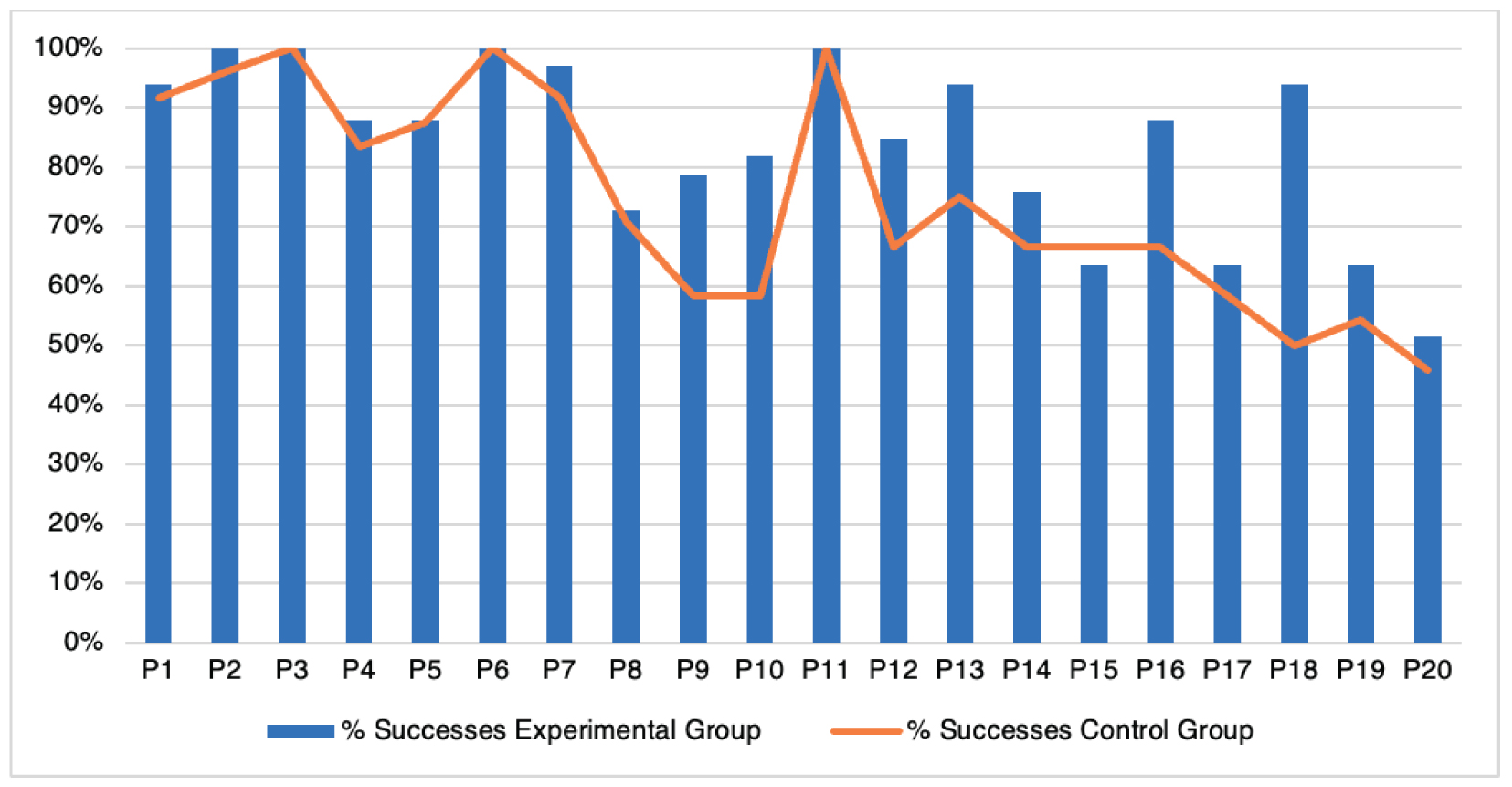 Figure 2
TEMT results for logical skills
Figure 2
TEMT results for logical skills
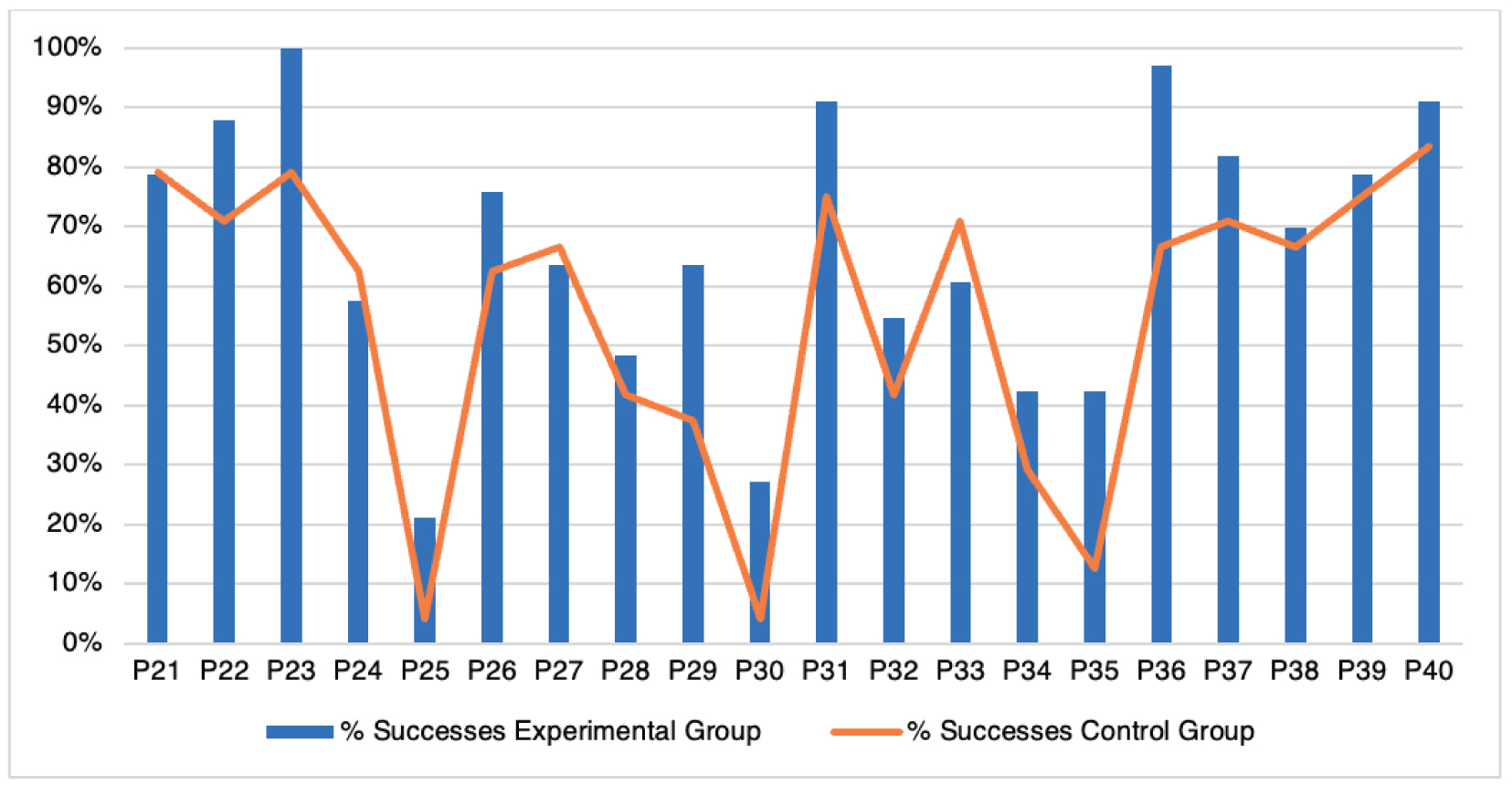 Figure 3
TEMT results for numerical skills
Figure 3
TEMT results for numerical skills
The items with lower scores in the experimental group are P15, P24, P27 and P33. Despite these differences found in favour of the control group, none of them are statistically significant. Table 5 lists those items that do show these differences in favour of the experimental group.
It is worth mentioning four items that show low scores in both groups, P25, P30, P34 and P35, all of them related to counting skills. These items coincide with the only items that are classified as “very difficult” in the TEMT manual, with a difficulty index below .25.
P25 asks for counting by twos up to 14; P30 aims at counting backwards from 17; P34 shows how children count 19 objects without the possibility of manipulation, while P35 aims at children counting up to 12 but as part of an additive strategy, giving first 5 objects to be hidden and then adding 7 more.
Table 5
Results of the items of the TEMT instrument that are statistically significant
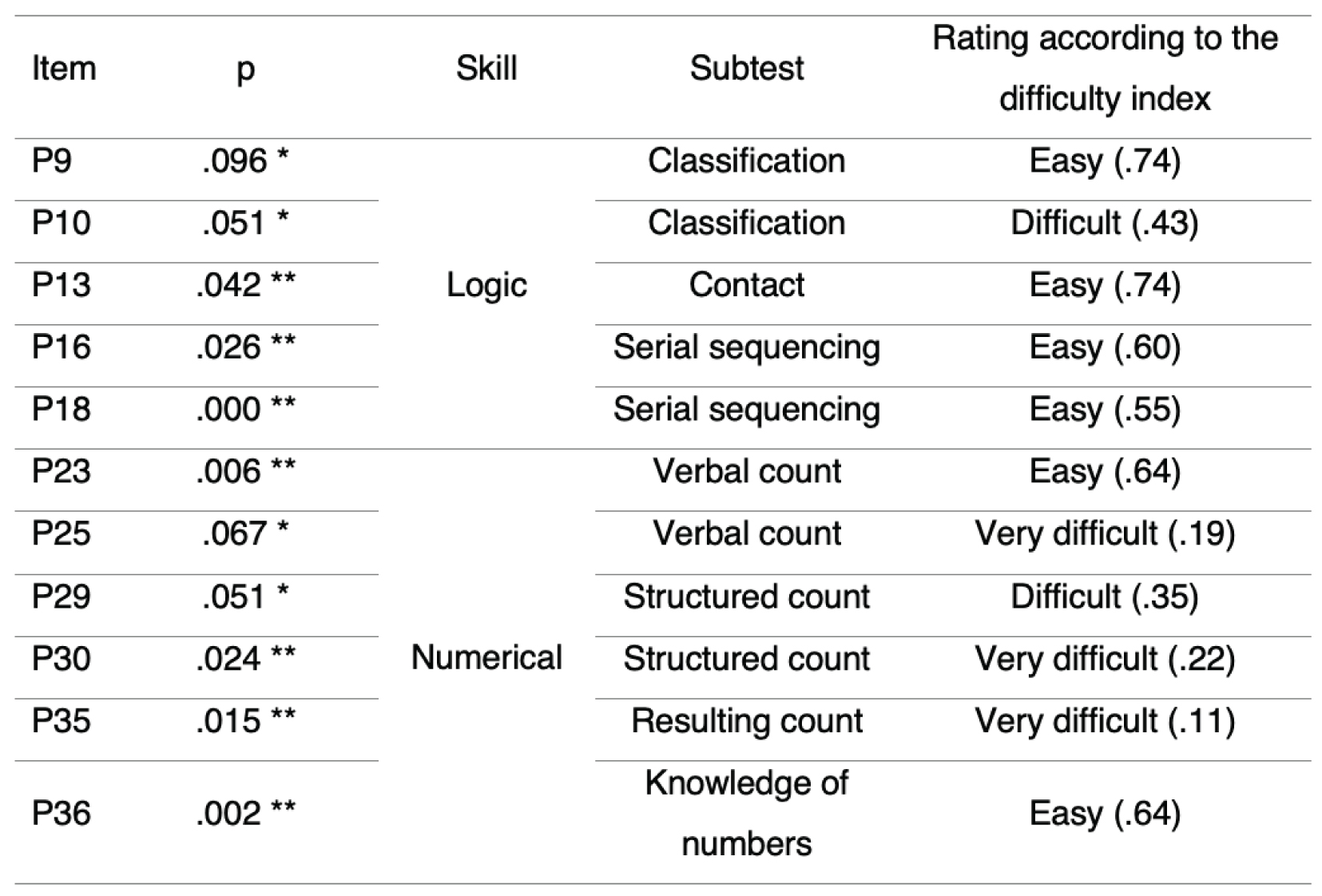
Note: *=p<.05
**=p<.10
As we can see, the significant differences, which always indicate better results in the experimental group, are slightly higher in the area corresponding to numerical work, with six items, compared to five in the logic area.
These differences occur in 3 of the 4 items considered to be the most difficult in the tool.
Items P15 and P24 (figure 4) focus attention on instructions where the representation used for objects is too compact. In P15, the child is asked to count the number of balloons and to point out which of the lower squares has the same number of dots (counting), and in P24 the child is asked to locate the 18th flower (ordinal).
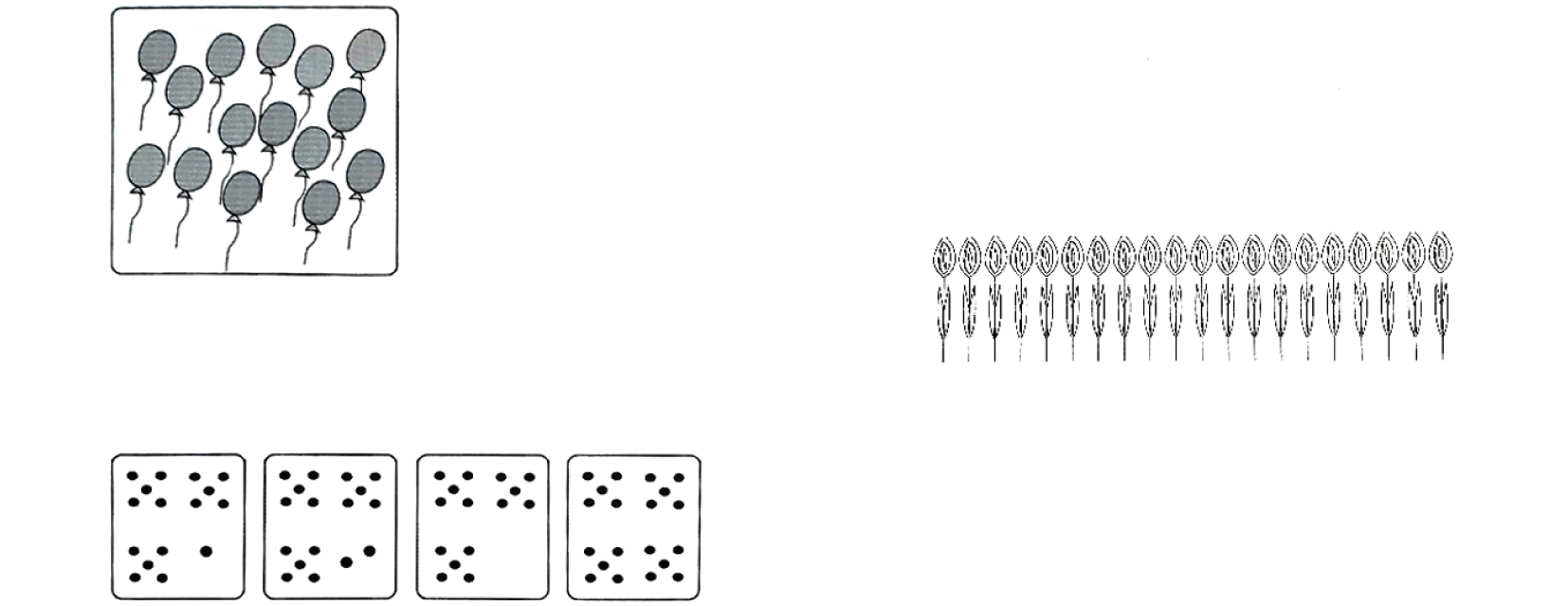 Figure 4
Evaluation sheet for items 15 and 24 of the TEMT, model A
Figure 4
Evaluation sheet for items 15 and 24 of the TEMT, model A
These results are confirmed when we calculate the NCM of each student in both groups, and are contrasted with a Student’s t-test, after checking the assumption of normality in the two groups (Kolmogorov-Smirnov tests with the Lilliefors and Shapiro-Wilk correction), obtaining significant differences with better overall results in the experimental group. Specifically, the mean takes a value of 30.5 in the experimental group and 25.9 in the control group, rejecting the null hypothesis of equality of means (p = .002).
With regard to differences by gender, the Chi-square test shows that there are few items with differential results (table 6). The girls obtain better the results in all of them.
Table 6
Results of the TEMT instrument items showing differences by gender

Note: *=p<.05
**=p<.10
Items P9 and P24 stand out in particular for the type of object they seek to identify, a handbag in item P9 (figure 5) and flowers in item P24.
 Figure 5
TEMT item 9 evaluation sheet, model A
Figure 5
TEMT item 9 evaluation sheet, model A
As for any potential impact of age, measured in days, it can be stated that this variable is not significant in the analysis. To test this, logistic regressions have been adjusted with age as an independent variable. In no case was significance found at 5% and in the few cases where there was significance at 10% (table 7) the impact was practically nil (beta coefficient of the logistic regression very close to 0).
Table 7
Results of the TEMT instrument items showing differences by age

We checked whether there were differences in relation to gender and age using the NCM value of each of the students for the two groups once again, and no significant differences were found in relation to either of the two variables. There is no significant statistical evidence to reject normality and equality of means (p=.740), and uncorrelatedness between NCM and age (p=.277).
In addition to the information provided by the tool, in the daily meetings between the teaching and research teams, other qualitative results of the experience - the result of classroom observation - could be assessed, such as the rapid and spontaneous acquisition of the linguistic expression of mathematical content by the children.
Discussion and conclusions
The initial specific objective was to develop the adaptation of a story to a specific scenario for the development of logical-mathematical thinking. The results from the different scenes of the story previously presented show this context as a facilitator for the early learning of mathematical contents. Math education can be enhanced if learning is placed in a context that facilitates social interactions, where children can construct knowledge from their experiences. (Sawatzki & Sullivan, 2018). This context can be built from the story told in the story as a connection with the child’s environment that motivates him/her to learn from curiosity and interest, facilitating the visualisation of mathematical concepts from concrete actions to more abstract contents. (Maričić et al., 2017).
One of the advantages of combining mathematics and literature in the EI classroom is that the two content areas are not disconnected, and that we can consider such interventions as a way to build understanding and enthusiasm and a way of discovering mathematical concepts” (Kribs & Ruebel, 2008, p. 36). Maintaining high levels of reading motivation can be beneficial from a reciprocal relationship with the reading ability (Hebbecker et al., 2019).
The second specific objective focused on determining the influence of the didactic experience on the achievement of mathematical competence shows more favourable results in the students who participated in the intervention with the story. These results stand out especially for the different counting strategies. These counting principles facilitate the subsequent possibilities of arithmetic calculations without the need for counting (Jordan & Dyson, 2013). Better results are observed in 27.5% of the items of the instrument in the experimental group, while the rest have the same results.
In the four subtests of logical skills, we can point to improvements in classification and serial sequencing, fundamentally in accordance with the type of activities presented, especially those carried out in individual format. As for the results in numerical skills, the results in verbal counting stand out, fundamentally in the sequence of number words, both one by one and two by two.
It should also be noted in this block that the items considered to be the most difficult in the instrument for this age group show significant differences in favour of the experimental group in three of them (P25, P30 and P35). The results in items P25 and P30 focused on the last two levels of acquisition of the numerical sequence, numerable chain level and bidirectional chain level, can be justified from the work of systematisation of the numerical sequence from the ordinal context (Fernández, 2016).
In those items related to general knowledge of numbers, shown from a verbal problem, we found improvements in one of the items of the block (P36), an aspect that has been worked on from the recreation of problem situations in group activities with the story.
The comparative results of the overall score of the instrument as a level of mathematical competence indicate better results in the experimental group.
In relation to the objective of analysing mathematical learning, using gender and age as differential variables, we can say that few differences have been observed, coinciding with previous research (Alsina & Berciano, 2018; Navarro et al., 2010).
Although the research has achieved its specific and thus its general objectives, demonstrating the usefulness of the use of storytelling in early mathematics learning, reflection is needed for future research, given that it has been carried out with a small sample size. It would also be advisable to carry it out over a longer intervention period and with more than one story to check the effects of the story, and even of the type of materials used or the use of stories specifically constructed for learning mathematics. We also find it advisable to review the instrument used, given that some results are conditioned by the typology of the illustrations on the objects to be counted. Any future research should also include in this type of intervention the assessment of geometry-related content, along the same lines as the recommendations made in recent research (Assel et al., 2020), based on the consideration of geometry as a basis for the development of more abstract reasoning (Geary, 2007).
References
Alsina, A. (2012). Cómo desarrollar el pensamiento matemático de 0 a 6 años. Octaedro.
Alsina, A., & Berciano, A. (2018). Developing informal mathematics in early childhood education. Early Child Development and Care, 1-19. https://doi.org/10.1080/03004430.2018.1555823
Andersen, H. C. (1843). Den grimme ælling [El Patito Feo]. Nye eventyr. Første Bind. Første Samling.
Arens, A. K., Marsh, H. W., Craven, R. G., Yeung, A. S., Randhawa, E., & Hasselhorn, M. (2016). Math self-concept in preschool children: Structure, achievement relations, and generalizability across gender. Early Childhood Research Quarterly, 36, 391-403. https://doi.org/10.1016/j.ecresq.2015.12.024
Aragón, E. L., Delgado, C. I., Aguilar, M., Araújo, A., & Navarro, J. I. (2015). Estudio de la influencia de la inteligencia y el género en la evaluación matemática temprana. European journal of education and psychology, 6(1). https://doi.org/10.30552/ejep.v6i1.90
Assel, M. A., Montroy, J. J., Williams, J. M., Foster, M., Landry, S. H., Zucker, T., Crawford, A., Hyatt, H., & Bhavsar, V. (2020). Initial Validation of a Math Progress Monitoring Measure for Prekindergarten Students. Journal of Psychoeducational Assessment, 1-19. https://doi.org/10.1177/0734282920922078
Aymerich, C. (2010). Una mà de contes matemàtics. Biaix, 28-29, 32-36.
Bakker, M., Torbeyns, J., Wijns, N., Verschaffel, L., & De Smedt, B. (2019). Gender equality in 4-to 5-year-old preschoolers’ early numerical competencies. Developmental science, 22(1), e12718. https://doi.org/10.1111/desc.12718
Barrera, H. (2012). Cuéntamemates. Beginbook Ediciones.
Bender, A., & Beller, S. (2012). Nature and culture of finger counting: Diversity and representational effects of an embodied cognitive tool. Cognition, 124(2), 156-182. https://doi.org/10.1016/j.cognition.2012.05.005
Bevins, S., & Price, G. (2016). Reconceptualising inquiry in science education. International Journal of Science Education, 38(1), 17-29. https://doi.org/10.1080/09500693.2015.1124300
Borzone, A. M. (2005). La Lectura de Cuentos en el Jardín Infantil: Un Medio Para el Desarrollo de Estrategias Cognitivas y Lingüísticas. Psykhe (Santiago), 14(1), 192-209. https://doi.org/10.4067/S0718-22282005000100015
Brousseau G. (1998). Théorie des Situations Didactiques. La Pensée Sauvage.
Cai, H., Lin, L., & Gu, X. (2016). Using a semantic diagram to structure a collaborative problem solving process in the classroom. Educational Technology Research and Development, 64, 1207–1225. https://doi.org/10.1007/s11423-016-9445-6
Carney, R. N., & Levin, J. R. (2002). Pictorial Illustrations Still Improve Students' Learning from Text. Educational Psychology Review, 14, 5-26. https://doi.org/10.1023/A:1013176309260
Campbell, J. (1984). El héroe de las mil caras. Psicoanálisis del mito. Fondo de cultura económica.
Cascallana, M. T. (1988). Iniciación a la matemática. Materiales y recursos didácticos. Santillana.
Cerrillo, P. (2007). Literatura Infantil y Juvenil y educación literaria: Hacia una nueva enseñanza de la literatura. Octaedro.
Claessens, A., & Engel, M. (2013). How important is where you start? Early mathematics knowledge and later school success. Teachers College Record, 115, 1-29.
Clements, D. H., & Sarama, J. (2014). Learning and teaching early math: The learning trajectories approach. Routledge. https://doi.org/10.4324/9780203520574
Colomer, T., & Ramos, N. (2002). Treballem matemàtiques amb els contes populars. Biaix, 20, 20-25.
Decreto 17/2008, de 6 de marzo, del Consejo de Gobierno, por el que se desarrollan para la Comunidad de Madrid las enseñanzas de la Educación Infantil. Boletín Oficial de la Comunidad de Madrid, 73, 13-16. https://www.bocm.es/boletin/CM_Orden_BOCM/2018/03/26/BOCM-20180326-1.PDF
Fernández, C. (2016). Una propuesta didáctica para trabajar la secuencia numérica en el segundo ciclo de educación infantil. Enseñanza de las ciencias, 34(2), 185-204. https://doi.org/10.5565/rev/ensciencias.1798
Fernández, C. (2018). Pensamiento numérico: evolución del número cardinal en Educación Infantil. Educação Matemática Debate, 2(5), 188-204. https://doi.org/10.24116/emd25266136v2n52018a03
Follmer, A., & Semb, P. A. (2008). Do illustrations enhance preschoolers’ memories for stories? Age-related change in the picture facilitation effect. Journal of Experimental Child Psychology, 99(4), 271-287. https://doi.org/10.1016/j.jecp.2007.06.005
Geary, D. C. (2007). An evolutionary perspective on learning disability in mathematics. Developmental Neuropsychology, 32, 471-519. https://doi.org/10.1080/87565640701360924
Ginsburg, H. P., & Golbeck, S. L. (2004). Thoughts on the future of research on mathematics and science learning and education. Early childhood research quarterly, 19(1), 190-200. https://doi.org/10.1016/j.ecresq.2004.01.013
Hannula-Sormunen, M.M., McMullen, J., & Lehtinen E. (2019). Everyday Context and Mathematical Learning: On the Role of Spontaneous Mathematical Focusing Tendencies in the Development of Numeracy. In A. Fritz, V. Haase, & P. Räsänen (Eds.), International Handbook of Mathematical Learning Difficulties. Springer. https://doi.org/10.1007/978-3-319-97148-3_3
Hassinger-Das, B., Jordan, N. C., & Dyson, N. (2015). Reading stories to learn math: Mathematics vocabulary instruction for children with early numeracy difficulties. The Elementary School Journal, 116(2), 242-264. https://doi.org/10.1086/683986
Haylock, D., & Cockburn, A. (2013) Understanding Mathematics in the Lower Primary Years. Paul Chapman.
Hebbecker, K., Förster, N., & Souvignier, E. (2019). Reciprocal effects between reading achievement and intrinsic and extrinsic reading motivation. Scientific Studies of Reading, 23(5), 419-436. https://doi.org/10.1080/10888438.2019.15984
Hong, H. (1996). Effects of mathematics learning through children's literature on math achievement and dispositional outcomes. Early childhood research quarterly, 11(4), 477-494. https://doi.org/10.1016/S0885-2006(96)90018-6
Kalogiannakis, M., Nirgianaki, G. M., & Papadakis, S. (2018). Teaching magnetism to preschool children: The effectiveness of picture story reading. Early Childhood Education Journal, 46(5), 535-546. https://doi.org/10.1007/s10643-017-0884-4
Keat, J. B., & Wilburne, J. M. (2009). The Impact of Storybooks on Kindergarten Children's Mathematical Achievement and Approaches to Learning. Online Submission, 6(7), 61-67.
Keuch, S., & Brandt, B. (2020). ‘You Are Already Bigger Than the Giraffe!’—The Use of Adjectives in Measurement Activities in Kindergarten. In M. Carlsen, I. Erfjord & P. Hundeland (Eds.). Mathematics Education in the Early Years. Springer. https://doi.org/10.1007/978-3-030-34776-5_22
Kribs, C. M., & Ruebel, K. K. (2008). Exploring mathematical concepts in literature. Middle School Journal, 40(1), 36-42. https://doi.org/10.1080/00940771.2008.11461663
Jacobi-Vessels, J.L., Todd Brown, E., Molfese, V.J., & Do, A. (2016). Teaching Preschoolers to Count: Effective Strategies for Achieving Early Mathematics Milestones. Early Childhood Education Journal, 44, 1-9. https://doi.org/10.1007/s10643-014-0671-4
Jordan, N. C., & Dyson, N. (2013). Number Sense Interventions. Paul H. Brookes Publishing.
Laski, E., Casey, B., Yu, Q., Dulaney, A., Heyman, M., & Dearing, E. (2013). Spatial skills as a predictor of first grade girls’ use of higher level arithmetic strategies. Learning and Individual Differences, 23(1), 123-130. https://doi.org/10.1016/j.lindif.2012.08.001
Locuniak, M. N., & Jordan, N. C. (2008). Using kindergarten number sense to predict calculation fluency in second grade. Journal of learning disabilities, 41(5), 451-459. https://doi.org/10.1177/0022219408321126
Makosz, S., Zambrzycka, J., & Kotsopoulos, D. (2019). The “Girl Crisis”: The Relationship Between Early Gender Differences and Future Mathematical Learning and Participation. In K. Robinson, H. Osana & D. Kotsopoulos (Eds.), Mathematical Learning and Cognition in Early Childhood. Springer. https://doi.org/10.1007/978-3-030-12895-1_2
Maričić, S. M., Stakić, M. M., & Malinović-Jovanović, N. T. (2018). The Role of Literary Content for Children in Preschool Mathematics Education. Eurasia Journal of Mathematics, Science and Technology Education, 14(2), 631-642. https://doi.org/10.12973/ejmste/80627
Mazzocco, M. M., & Thompson, R. E. (2005). Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice, 20(3), 142-155. https://doi.org/10.1111/j.1540-5826.2005.00129.x
National Association for the Education of Young Children (NAEYC), & National Council of Teachers of Mathematics (NCTM). (2002). Early childhood mathematics: Promoting good beginnings. A joint position statement. https://www.naeyc.org/sites/default/files/globally-shared/downloads/PDFs/resources/position-statements/psmath.pdf
Nanu, C., Laakkonena, E., & Hannula-Sormunen, M. (2020). The Effect of First School Years on Mathematical Skill Profiles. Frontline Learning Research, 8(1), 56-75. https://doi.org/10.14786/flr.v8i1.485
Navarro, J. I., Aguilar, M., García, M., Menacho, I., Marchena, E., & Alcalde, C. (2010). Diferencias en habilidades matemáticas tempranas en niños y niñas de 4 a 8 años. Revista española de pedagogía, 245, 85-98.
Navarro, J.I., Aguilar, M., Alcalde, C., Marchena, E., Ruiz, G., Menacho, I., & Sedeño, M. (2011). Test de Evaluación Matemática de Temprana (TEMT). Spanish version. Dpto de Psicología. EOS. Original version: Van Luit, J., Van de Rijt, B. & Pennings, A. (1998). The Utrecht Early Mathematical Competence Test. Graviant.
Nguyen, D., & Ryan, A. (2008). Does stereotype threat affect test performance of minorities and women? A meta-analysis of experimental evidence. Journal of Applied Psychology, 93, 1314-1334. https://doi.org/10.1037/a0012702
Nowell, A., & Hedges, L.V. (1998). Trends in gender differences in academic achievement from 1960-1994: An analysis of differences in mean, variance, and extreme scores. Sex Roles, 39, 21-43. https://doi.org/10.1023/A:1018873615316
Propp, V. (1981). Morfología del cuento. Fundamentos.
Reilly, D., Neumann, D.L., & Andrews, G. (2017) Gender Differences in Spatial Ability: Implications for STEM Education and Approaches to Reducing the Gender Gap for Parents and Educators. In M. Khine (Eds.), Visual-spatial Ability in STEM Education. Springer. https://doi.org/10.1007/978-3-319-44385-0_10
Riley, N., Lubans, D., Holmes, K., Hansen, V., Gore, J., & Morgan, P. (2017). Movement-based Mathematics: Enjoyment and Engagement without Compromising Learning through the EASY Minds Program. Eurasia Journal of Mathematics, Science and Technology Education, 13(6), 1653-1673. https://doi.org/10.12973/eurasia.2017.00690a
Rodríguez, A. I. (2016). Impact of Chronological Age Differences on the Academic Performance of Students in a First-Grade Classroom. Journal of Interdisciplinary Undergraduate Research, 8, Article 2, 1-23.
Rodríguez, M. M., & Fernández, N. (2016). Dinosaurios que comen uvas y viven en cuevas. El cardinal numérico. NÚMEROS. Revista de didáctica de las matemáticas, 91, 69-90.
Saá, M. D. (2002). Las matemáticas de los cuentos y las canciones. EOS.
Sánchez, L., Benítez, R., & Aguilar, S. (2018). El triángulo de la educación infantil: los cuentos, las emociones y las TIC. Hachetetepé. Revista científica de Educación y Comunicación, 16, 29-38. https://doi.org/10.25267/Hachetetepe.2018.v1.i16.4
Sawatzki, C., & Sullivan, P. (2018) Shopping for Shoes: Teaching Students to Apply and Interpret Mathematics in the Real World. International Journal of Science and Mathematics Education, 16, 1355–1373. https://doi.org/10.1007/s10763-017-9833-3
Swoboda, E., & Vighi, P. (2016). Early geometrical thinking in the environment of patterns, mosaics and isometries. Springer Nature. https://doi.org/10.1007/978-3-319-44272-3
White, J. (2017). Using Children’s Literature to Teach Problem Solving in Math Addressing the Standards for Mathematical Practice in K–5. Routledge.
Whitin, P., & Whitin, D. (2004). New Visions for Linking Literature and Mathematics. The National Council of Teachers of English
Author notes
* Contact: blanca.arteaga@edu.uned.es




























